Question

Suppose you believe that the true average daily trade volume for General Electric stock is 49,829,719 shares and a standard deviation of 21,059,637 shares. Considering a 95% confidence level: What is the minimum required sample size if you would like your sampling error to be limited to 1,000,000 shares

Answer 1

The minimum sample size is 1,704.

Explanation:

We have to find our
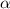`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.95)/(2) = 0.025`

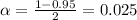
Now, we have to find z in the Z-table as such z has a p-value of
`1 - \alpha`.

That is z with a p-value of
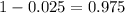`1 - 0.025 = 0.975`, so Z = 1.96.

Now, find the margin of error M as such

`M = z(\sigma)/(√(n))`

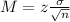
In which
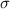`\sigma` is the standard deviation of the population and n is the size of the sample.

Standard deviation of 21,059,637 shares

This means that
`\sigma = 21059637`

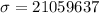
What is the minimum required sample size if you would like your sampling error to be limited to 1,000,000 shares?

This is n for which
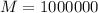`M = 1000000`, so:

`M = z(\sigma)/(√(n))`

`1000000 = 1.96(21059637)/(√(n))`

`1000000√(n) = 1.96*21059637`

`√(n) = (1.96*21059637)/(1000000)`

`(√(n))^2 = ((1.96*21059637)/(1000000))^2`

`n = 1703.8`

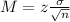
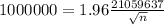
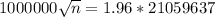
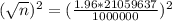
Rounding up:

The minimum sample size is 1,704.