Answer:
A
Explanation:
a geometric sequence is where we multiply a factor from element to element.
a1 = $900
a2 = 981 = a1 × f = 900 ×
a3 = 1069.29 = a2 × f = a1 × f × f = s1 × f²
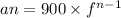
so, now let's try and get f.
remember, 981 = 900 × f
f = 981/900 = 109/100 = 1.09
just to control, we check for s3 :
900 × (1.09)² = 900 × 1.1881 = 1069.29
correct.
so,
a13 = 900 × (1.09)¹² = 2,531.398304
s13 is then the sum of all a1, ..., a13
there is a nice formula for sums of finite sequences
s13 = 900 × (1-f¹³) / (1-f) = 900×(1-(1.09)¹³) / (1-1.09) =
= 900×(1-3.065804612) / (-0.09) =
= 900×(-2.065804612) / (-0.09) = 20,658.04612
.