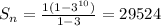Question

What is the sum of the geometric sequence 1, 3, 9, ... if there are 10 terms? (5 points)

Answer 1

`S_n = (1 (1 - 3^(10)))/(1 - 3) = 29524`

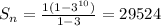
Explanation:

There's a handy formula we can use to find the sum of a geometric sequence, and here it is

`S_n = (a_1 (1 - r^n))/(1 - r)`

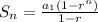
The value n represents the amount of terms you want to sum in the sequence. The variable r is known as the common ratio, and a is just some constant. Let's find those values.

First lets visualize this sequence

`n_1 = 1\\n_2 = 1 + 3\\n_3 = 1 + 3 + 3^2\\n_4=1+3+3^2+3^3\\...`

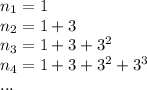
Okay so there's clearly a pattern here, let's write it a bit more concisely. For each n, starting at 1, we raise 3 to the (n-1) power, add it to what we had for the previous term.

`S_n = \sum{3^(n-1)} = 3^(1 - 1) + 3^(2 - 1) + 3^(3-1) ...`

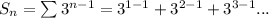
Our coefficients of r, and a, are already here! As you can see below, r is just 3, and a is just 1.

`S_n = \sum{a*r^(n-1)}`

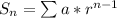
To finish up lets plug these coefficients in and get our sum after 10 terms.

`S_n = (1 (1 - 3^(10)))/(1 - 3) = 29524`