Question

2. Write the equation of the line parallel to y = -4x/3 + 5 thru (-6,1). Show all work.​

Answer 1

`\boxed {\boxed {\sf y= - (4)/(3) x -7}}`

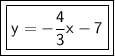
Explanation:

We can find the equation using the point-slope formula.

`y-y_1=m(x-x_1)`

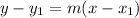
where (x₁, y₁) is the point and m is the slope.

We already know the point is (-6,1). We must find the slope.

We are told the line is parallel to y=-4x/3 +5. Since this line is in y=mx+b form, the slope (m) must be -4/3. Parallel lines have equal slopes, so the line we are finding also has a slope of -4/3

Next, define values for the variables.

`x_1= -6 \\y_1= 1\\m= - (4)/(3)`

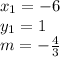
Substitute the values into the formula.

`y-1= - (4)/(3) (x--6)`

`y-1= - (4)/(3) (x+6)`

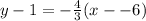
Now put the equation into the form y=mx+b. First, distribute the -4/3 .

`y-1= - (4)/(3) *x+ - \frac {4}{3}*6`

`y-1= - (4)/(3) x - 8`

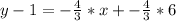
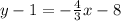
Add 1 to both sides to isolate y.

`y-1+1= - (4)/(3) x - 8+1`

`y= - (4)/(3) x -7`

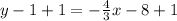
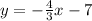
The equation of the line is y=-4/3x -7