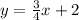Answer (assuming it can be in slope-intercept form):
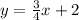
Explanation:
When knowing the y-intercept and a slope of a line, you can write its equation in slope-intercept form, or y = mx + b format.
1) First, find the slope. Use two points from the graph. We can see that the points (0,2) and (4,5) are on the line, therefore substitute their x and y values into the slope formula
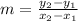 and solve:
and solve:
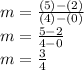
Thus, the slope is
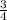 .
.
2) Next, find the y-intercept of the line by looking at the graph. The y-intercept is the point at which the line intersects the y-axis. By reading the graph, we can see that that point is (0,2), thus 2 is the y-intercept.
3) Now, using the slope-intercept formula
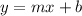 , substitute the found values for the
, substitute the found values for the
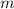 and the
and the
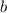 to write the equation of the line.
to write the equation of the line.
Since
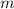 represents the slope, substitute
represents the slope, substitute
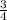 in its place. Since
in its place. Since
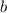 represents the y-intercept, substitute 2 in its place. This gives the following answer and equation:
represents the y-intercept, substitute 2 in its place. This gives the following answer and equation: