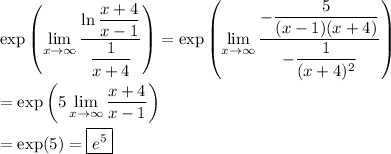It looks like the limit you want to find is

One way to compute this limit relies only on the definition of the constant e and some basic properties of limits. In particular,
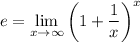
The idea is to recast the given limit to make it resemble this definition. The definition contains a fraction with x as its denominator. If we expand the fraction in the given limand, we have a denominator of x - 1. So we rewrite everything in terms of x - 1 :
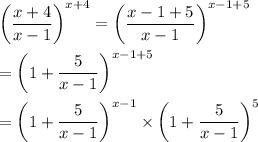
Now in the first term of this product, we substitute y = (x - 1)/5 :

Then use a property of exponentiation to write this as
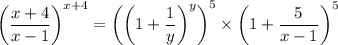
In terms of end behavior, (x - 1)/5 and x behave the same way because they both approach ∞ at a proportional rate, so we can essentially y with x. Then by applying some limit properties, we have
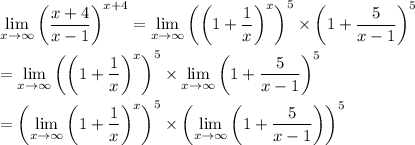
By definition, the first limit is e and the second limit is 1, so that
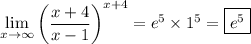
You can also use L'Hopital's rule to compute it. Evaluating the limit "directly" at infinity results in the indeterminate form
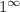 .
.
Rewrite
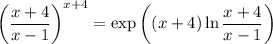
so that

and now evaluating "directly" at infinity gives the indeterminate form 0/0, making the limit ready for L'Hopital's rule.
We have
![(\mathrm d)/(\mathrm dx)\left[\ln(x+4)/(x-1)\right] = -\frac5{(x-1)^2}*(1)/((x+4)/(x-1)) = -\frac5{(x-1)(x+4)}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/fgntleb7h06e3es0uo40as.png)
![(\mathrm d)/(\mathrm dx)\left[\frac1{x+4}\right]=-\frac1{(x+4)^2}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/oiyw26ek6e3meqy9zusxr8.png)
and so