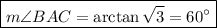Answer:
Part 1)
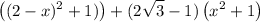
Or simplified:
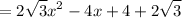
Part 2)
The value of x for which the given expression will be the lowest is:
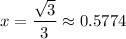
And the magnitude of ∠BAC is 60°.
Explanation:
We are given a ΔABC with an area of one. We are also given that AB = 2, BC = a, and CA = b. CD is a perpendicular line from C to AB.
Please refer to the diagram below.
Part 1)
Since we know that the area of the triangle is one:
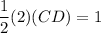
Simplify:

From the Pythagorean Theorem:
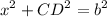
Substitute:
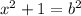
BD will simply be (2 - x). From the Pythagorean Theorem:
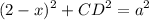
Substitute:
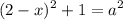
We have the expression:
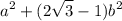
Substitute:
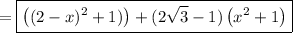
Part 2)
We can simplify the expression. Expand and distribute:

Simplify:
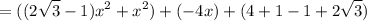
Simplify:
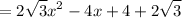
Since this is a quadratic with a positive leading coefficient, it will have a minimum value. Recall that the minimum value of a quadratic always occur at its vertex. The vertex is given by the formulas:
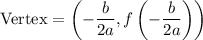
In this case, a = 2√3, b = -4, and c = (4 + 2√3).
Therefore, the x-coordinate of the vertex is:
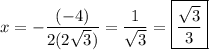
Hence, the value of x at which our expression will be the lowest is at √3/3.
To find ∠BAC, we can use the tangent ratio. Recall that:
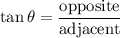
Substitute:
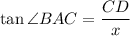
Substitute:
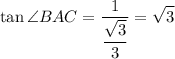
Therefore: