Question

A quality control engineer at a potato chip company tests the bag filling machine by weighing bags of potato chips. Not every bag contains exactly the same weight. But if more than 16% of bags are over-filled then they stop production to fix the machine. They define over-filled to be more than 1 ounce above the weight on the package. The engineer weighs 94 bags and finds that 16 of them are over-filled. He plans to test the hypotheses H 0 : p = 0.11 versus H a : p > 0.11. What is the test statistic?

Answer 1

The test statistic is z = 1.865.

Explanation:

The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

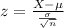
In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
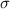`\sigma` is the standard deviation and n is the size of the sample.

H0: p = 0.11

This means that 0.11 is tested at the null hypothesis, and so:

`\mu = 0.11`

`\sigma = √(0.11*0.89) = 0.3129`

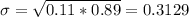
The engineer weighs 94 bags and finds that 16 of them are over-filled.

This means that:

`n = 94, X = (16)/(94) = 0.1702`

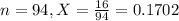
What is the test statistic?

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.1702 - 0.11)/((0.3129)/(√(94)))`

`z = 1.865`

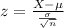
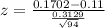
The test statistic is z = 1.865.