Answer:
S₁₀₀ = 15050
Explanation:
There is a common difference between consecutive terms
5 - 2 = 8 - 5 = 3
This indicates the sequence is arithmetic with sum to n terms
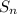 =
=
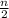 [ 2a₁ + (n - 1)d ]
[ 2a₁ + (n - 1)d ]
where a₁ is the first term and d the common difference
Here a₁ = 2 and d = 3 , then
S₁₀₀ =
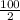 [ (2 × 2) + (99 × 3) ]
[ (2 × 2) + (99 × 3) ]
= 50 (4 + 297)
= 50 × 301
= 15050