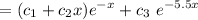Question

Use the procedures developed to find the general solution of the differential equation. (Let x be the independent variable.)

2y''' + 15y'' + 24y' + 11y= 0

Answer 1

Given :

2y''' + 15y'' + 24y' + 11y= 0

Let x = independent variable

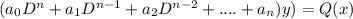`(a_0D^n + a_1D^(n-1)+a_2D^(n-2) + ....+ a_n) y) = Q(x)` is a differential equation.

If
`Q(x) \\eq 0`

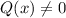
It is non homogeneous then,

The general solution = complementary solution + particular integral

If Q(x) = 0

It is called the homogeneous then the general solution = complementary solution.

2y''' + 15y'' + 24y' + 11y= 0

`$(2D^3+15D^2+24D+11)y=0$`

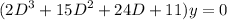
Auxiliary equation,

`$2m^3+15m^2+24m +11 = 0$`

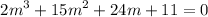
-1 | 2 15 24 11

| 0 -2 - 13 -11

2 13 11 0

∴
`2m^2+13m+11=0`

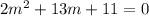
The roots are

`$=(-b\pm √(b^2-4ac))/(2a)$`

`$=(-13\pm √(13^2-4(11)(2)))/(2(2))$`

`$=(-13\pm9)/(4)$`

`$=-5.5, -1$`

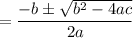
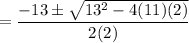
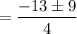
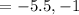
So,
`m_1, m_2, m_3 = -1, -1, -5.5`

Then the general solution is :

`$= (c_1+c_2 x)e^(-x) + c_3 \ e^(-5.5x)$`