Answer:
The family of directions of the given vector is represented by
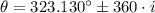 ,
,
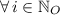 .
.
Explanation:
According to the given information, vector stands in the 4th Quadrant (
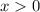 ,
,
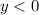 ) and direction of the vector (
) and direction of the vector (
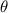 ) in sexagesimal degrees, is determined by following definition:
) in sexagesimal degrees, is determined by following definition:
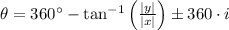 ,
,
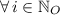
Please notice that angle represents a function with a periodicity of 360°.
If we know that
 and
and
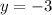 , then the direction of the vector is:
, then the direction of the vector is:

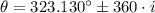
The family of directions of the given vector is represented by
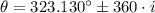 ,
,
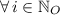 .
.