Question

Express this to single logarithm


`(1)/(2) log_(2)(m) - 3 log_(2)(n) + 2 log(q)`
​

Answer 1

Answer:
`\log_(2)\left((q^2√(m))/(n^3)\right)`

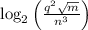
We have something in the form log(x/y) where x = q^2*sqrt(m) and y = n^3. The log is base 2.

===========================================================

Step-by-step explanation:

It seems strange how the first two logs you wrote are base 2, but the third one is not. I'll assume that you meant to say it's also base 2. Because base 2 is fundamental to computing, logs of this nature are often referred to as binary logarithms.

I'm going to use these three log rules, which apply to any base.

1. log(A) + log(B) = log(A*B)
2. log(A) - log(B) = log(A/B)
3. B*log(A) = log(A^B)

From there, we can then say the following:

`(1)/(2)\log_(2)\left(m\right)-3\log_(2)\left(n\right)+2\log_(2)\left(q\right)\\\\\log_(2)\left(m^(1/2)\right)-\log_(2)\left(n^3\right)+\log_(2)\left(q^2\right) \ \text{ .... use log rule 3}\\\\\log_(2)\left(√(m)\right)+\log_(2)\left(q^2\right)-\log_(2)\left(n^3\right)\\\\\log_(2)\left(√(m)*q^2\right)-\log_(2)\left(n^3\right) \ \text{ .... use log rule 1}\\\\\log_(2)\left((q^2√(m))/(n^3)\right) \ \text{ .... use log rule 2}`