Question

Phosphorus-32 is radioactive and has a half life of 14.3 days. Calculate the activity of a 3.5mg sample of phosphorus-32. Give your answer in becquerels and in curies. Round your answer to 2 significant digits.

Answer 1

The activity of P-32 is 3.7x10¹³ becquerels = 1.0x10³ curies.

Step-by-step explanation:

The activity of P-32 can be calculated with the following equation:

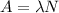`A = \lambda N` (1)

Where:

N: is the number of atoms of P-32

λ: is the decay constant

We can find the number of atoms of P-32 as follows:

`N = (N_(A)*m)/(M)` (2)

Where:

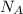`N_(A)`: is the Avogadro's number = 6.022x10²³ atoms/mol

m: is the mass of P-32 = 3.5x10⁻³ g

M: is the molar mass of the radionuclide (P-32) = 32 g/mol

Now, the decay constant is given by:

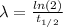`\lambda = (ln(2))/(t_(1/2))` (3)

Where:

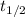`{t_(1/2)}`: is the half-life of P-32 = 14.3 days

Finally, we can find the activity of P-32 by entering equations (2) and (3) into (1):

`A = \lambda N = (ln(2))/(t_(1/2))*(N_(A)*m)/(M) = (ln(2))/(14.3 d*(24 h)/(1 d)*(3600 s)/(1 h))*(6.022 \cdot 10^(23) mol^(-1)*3.5 \cdot 10^(-3) g)/(32 g/mol) = 3.7 \cdot 10^(13) dis/s`

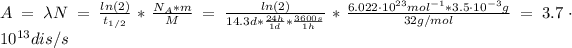
Since a becquerel (Bq) is defined as a disintegration (dis) per second, the activity in Bq is:

`A = 3.7 \cdot 10^(13) Bq`

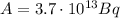
And, since a Curie (Ci) is 3.7x10¹⁰ Bq, the activity in Ci is:

`A = 3.7 \cdot 10^(13) Bq*(1 Ci)/(3.7 \cdot 10^(10) Bq) = 1.0 \cdot 10^(3) Ci`

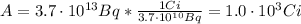
Therefore, the activity of P-32 is 3.7x10¹³ becquerels = 1.0x10³ curies.

I hope it helps you!