Answer:
their distance is increasing at the rate of 41.6 miles/hr
Explanation:
Given the data in the question;
first we determine the distance travelled by the first boat in 10 min when the second boat was crossing its path;
⇒ ( 30/60 ) × 10 = 5 miles
so as illustrated in the diagram below;
y² = x² + ( x + 5 )²
2y
 = 2x
= 2x
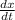 + 2(x+5)
+ 2(x+5)
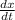
y
 = ( 2x + 5 ) ]
= ( 2x + 5 ) ]
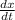
 = [( 2x + 5 )/y ]
= [( 2x + 5 )/y ]
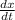 ------ let this be equation 1
------ let this be equation 1
Now, given that,
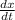 = 30 miles/hr, when x = 10
= 30 miles/hr, when x = 10
so
y = √( 10² + 15² ) = √325
so from equation 1
 = [( 2x + 5 )/y ]
= [( 2x + 5 )/y ]
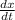
we substitute
 = [( 2(10) + 5 ) / √325 ]30
= [( 2(10) + 5 ) / √325 ]30
 = [ 25 / √325 ] × 30
= [ 25 / √325 ] × 30
 = 41.6 miles/hr
= 41.6 miles/hr
Therefore, their distance is increasing at the rate of 41.6 miles/hr