Hi there!
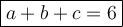
We can begin by using the point (0, 1).
At the graph's y-intercept, where x = 0, y = 1, so:
1 = a(0)² + b(0) + c
c = 1
We can now utilize the first point given (-3, 10):
10 = a(-3)² + b(-3) + 1
Simplify:
9 = 9a - 3b
Divide all terms by 3:
3 = 3a - b
Rearrange to solve for a variable:
b = 3a - 3
Now, use the other point:
15 = a(2)² + 2(3a - 3) + 1
14 = 4a + 6a - 6
Solve:
20 = 10a
2 = a
Plug this in to solve for b:
b = 3a - 3
b = 3(2) - 3 = 3
Add all solved variables together:
2 + 3 + 1 = 6