Question

Un grupo de estudiantes se junta a celebrar el termino del semestre, para lo que acuerdan preoarar un curanto. Reunen todos los ingredientes y los ponen en una olla y le aplican fuego hasta que esta alcanza una temperatura de 175°C. En este momento retiran la olla del fuego y queda expuesta a la temperatura ambiental, que es de 12°C

Answer 1

El problema esta incompleto, pero es facil ver que se desea estudiar el enfriamiento de la olla.

Sabemos que la ecuación de enfriamiento de Newton es:

`T (t) = T_s + (T_0 - T_s)*e^(-k*t)`

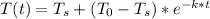
Donde t es el tiempo.

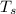`T_s` es la temperatura del ambiente, en este caso es 12°C

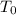`T_0` es la temperatura inicial del objeto, en este caso 175°C

k es una constante, que es lo que usualmente se pide obtener en este tipo de problemas.

Reemplazando esos valores en nuestra ecuación obtenemos:

`T(t) = 12 + (175 - 12)*e^(-k*t)\\\\T(t) = 12 + (163)*e^(-k*t)`

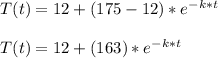
Ahora se nos dice:

"Luego de 10 minutos, la temperatura de la olla será de 100°C"

(estos valores no son necesariamente los del problema, son unos valores genéricos para poder mostrar como se resuelve este tipo de ejercicio)

Entonces, T(10 min) = 100°C

Reemplazando eso en nuestra ecación, obtenemos:

`T(10 min) = 100 = 12 + (163)*e^(-k*10min)`

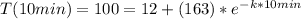
Ahora podemos despejar el valor de k resolviendo la ecuación de arriba.

`100 - 12 = (163)*e^(-k*10min)\\\\88 = (163)*e^(-k*10min)\\\\88/163 = e^{{-k*10min}`

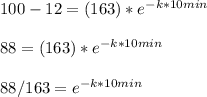
Ahora podemos recordar que:

ln(e^x) = x

Entonces aplicando el logaritmo natural a ambos lados, obtenemos:

`ln(88/163) = ln(e^(-k*10min)) = -k*10min\\\\ln(88/163)/(-10 min) = k = 0.062 min^(-1)`

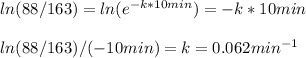
Así hemos encontrado el valor de k, y con exactamente el mismo método podríamos encontrar k en cualquier situación de este tipo.