Answer:
k = 11/3
Explanation:
If the line is tangent to the curve, then Δ = 0.
______________
Remembering:
Δ>0 two different points of intersection x'
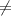 x''
x''
Δ=0 one point of intersection x' = x''
Δ<0 two different points of intersection in the complex plan x' and -x'
______________
As the line and the curve have one point of intersection, which is (x, y), we can make a equality between them:
2x + k = 3x² + 4
0 = 3x² - 2x + (4 - k)
Now we can use the Δ=0 (Δ= b² - 4ac)
Δ = 0 = (-2)² - 4.3.(4-k)
0 = 4 - 48 + 12k
12k = 44
k = 44/12 = 2 . 22 /3. 2.2 = 22/3.2 = 11/3
k = 11/3