Question

The function f(x) = −x2 + 18x − 72 models the daily profit, in dollars, a gym makes for selling memberships, where x is the number of memberships sold, and f(x) is the amount of profit.

Part A: Determine the vertex. What does this calculation mean in the context of the problem? (5 points)

Part B: Determine the x-intercepts. What do these values mean in the context of the problem? (5 points)

(10 points)

Answer 1

Explanation:

The way to do this so as to streamline both the vertex and finding the zeros is to complete the square. That method will provide us with the vertex, and then we can continue on to factor from that form to find the zeros. Completing the square requires us to set the quadratic equal to 0 then move over the constant, giving us

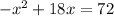`-x^2+18x=72` The leading coefficient HAS to be a positive 1; ours is negative 1 so we factor out the negative to get:

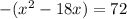`-(x^2-18x)=72` Now we're ready to complete the square.

Take half the linear term, square it, and add it to both sides. Our linear term is 18 (from -18x; don't worry about the negative because squaring it makes it positive anyway). Half of 18 is 9, and 9 squared is 81.

BUT on the left we have that -1 sitting out front that refuses to be ignored. What we actually added on to the left side, inside the parenthesis, is -1(81) which is -81. -81 is what we add to the right since that turns out to be what we added to the left:

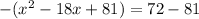`-(x^2-18x+81)=72-81` and we clean that up.

The reason we complete the square is because when we simplify the left side, we end up with a perfect square binomial found from taking the square root of x-squared, the first sign we come to, then the square root of 81:

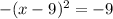`-(x-9)^2=-9`. Move the constant back over to get

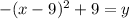`-(x-9)^2+9=y` telling us that the vertex is (9, 9). In the context of the problem that means that the gym sells on average 9 memberships a day and the profit it makes on average per day is $9.

To factor, we will go back one step to

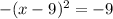`-(x-9)^2=-9` and begin by dividing both sides by -1 to get

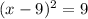`(x-9)^2=9` and undo the squaring by taking the square root of both sides to get

x - 9 = ±3 so

x = 9 + 3 and

x = 9 - 3 so

x = 6 and 12

Those are the zeros. This means that if they sell either 6 or 12 memberships they have a 0 profit. That may sound strange, but in business it does often work like that...selling too many of something makes your company lose money (this is often due to the cost required by you to produce or manufacture the product).