Question

150 mL of 0.25 mol/L magnesium chloride solution and 150 mL of 0.35 mol/L silver nitrate solution are mixed together. After reaction is completed; calculate the concentration of nitrate ions in solution. Assume that the total volume of the solution is 3.0 x 10^2 mL

Answer 1

`0.175\; \rm mol \cdot L^(-1)`.

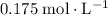Step-by-step explanation:

Magnesium chloride and silver nitrate reacts at a
`2:1` ratio:

`\rm MgCl_2\, (aq) + 2\, AgNO_3\, (aq) \to Mg(NO_3)_2 \, (aq) + 2\, AgCl\, (s)`.

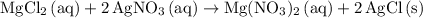In reality, the nitrate ion from silver nitrate did not take part in this reaction at all. Consider the ionic equation for this very reaction:

`\begin{aligned}& \rm Mg^(2+) + 2\, Cl^(-) + 2\, Ag^(+) + 2\, {NO_3}^(-) \\&\to \rm Mg^(2+) + 2\, {NO_3}^(-) + 2\, AgCl\, (s)\end{aligned}`.

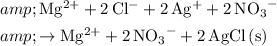The precipitate silver chloride
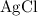`\rm AgCl` is insoluble in water and barely ionizes. Hence,
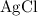`\rm AgCl\!` isn't rewritten as ions.

Net ionic equation:

`\begin{aligned}& \rm Ag^(+) + Cl^(-) \to AgCl\, (s)\end{aligned}`.

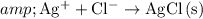Calculate the initial quantity of nitrate ions in the mixture.

`\begin{aligned}n(\text{initial}) &= c(\text{initial}) \cdot V(\text{initial}) \\ &= 0.25\; \rm mol \cdot L^(-1) * 0.150\; \rm L \\ &= 0.0375\; \rm mol \end{aligned}`.

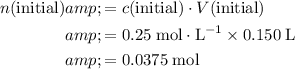Since nitrate ions
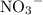`\rm {NO_3}^(-)` do not take part in any reaction in this mixture, the quantity of this ion would stay the same.

`n(\text{final}) = n(\text{initial}) = 0.0375\; \rm mol`.

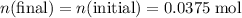However, the volume of the new solution is twice that of the original nitrate solution. Hence, the concentration of nitrate ions in the new solution would be
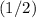`(1/2)` of the concentration in the original solution.

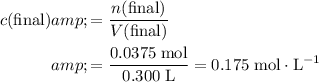`\begin{aligned} c(\text{final}) &= \frac{n(\text{final})}{V(\text{final})} \\ &= (0.0375\; \rm mol)/(0.300\; \rm L) = 0.175\; \rm mol \cdot L^(-1)\end{aligned}`.