Answer:
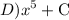
Explanation:
we would like to integrate the following Integral:
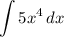
well, to get the constant we can consider the following Integration rule:
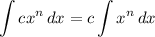
therefore,
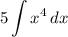
recall exponent integration rule:
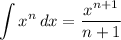
so let,
Thus integrate:
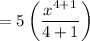
simplify addition:
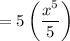
reduce fraction:
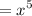
finally we of course have to add the constant of integration:
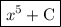
hence,
our answer is D)