Answer:
There would be
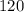 of them.
of them.
Explanation:
There are
 distinct letters in the word "
distinct letters in the word "
 ".
".
Hence, there would
 possible choices for the first letter that was selected.
possible choices for the first letter that was selected.
Since the chosen card won't be placed back in the pool, there would be only
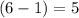 possible choices for the second letter.
possible choices for the second letter.
Likewise, there would be
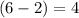 choices for the third letter.
choices for the third letter.
 . In other words, there are
. In other words, there are
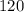 possible ways to draw three cards out of
possible ways to draw three cards out of
 one after another.
one after another.
Since the question states that the order of the cards matters, it won't be necessary to eliminate repetitions such as "
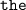 " and "
" and "
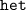 " from the number of combinations.
" from the number of combinations.