Answer:
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx = -93](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/c6ik0rsv3rvihole1p2sqs.png)
General Formulas and Concepts:
Calculus
Integration
Integration Property [Multiplied Constant]:
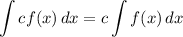
Integration Property [Addition/Subtraction]:
![\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/h405xx0sspogqoahw2d7bs.png)
Explanation:
Step 1: Define
Identify
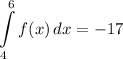
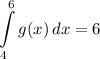
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/yb09qb48mdzpay8ppk5ynb.png)
Step 2: Integrate
- [Integral] Rewrite [Integration Property - Addition/Subtraction]:
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx = \int\limits^6_4 {3f(x)} \, dx - \int\limits^6_4 {7g(x)} \, dx](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/8nt921jg71bgm031icwev6.png)
- [Integrals] Rewrite [Integration Property - Multiplied Constant]:
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx = 3 \int\limits^6_4 {f(x)} \, dx - 7 \int\limits^6_4 {g(x)} \, dx](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/2c48cj33ho3lahft2xw2x2.png)
- [Integrals] Substitute:
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx = 3(-17) - 7(6)](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/gtqj0l1kneiveonnyl2n1l.png)
- Simplify:
![\displaystyle \int\limits^6_4 {[3f(x) - 7g(x)]} \, dx = -93](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/c6ik0rsv3rvihole1p2sqs.png)
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Integration