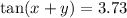Answer:
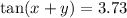
Step-by-step explanation:
The missing part of the question are:
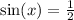
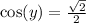
Required
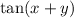
First, we calculate
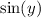 and
and
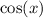
We have:
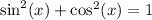
So:
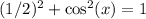
Collect like terms
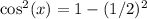
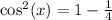
Take LCM
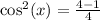
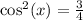
Square roots of both sides
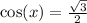
Similarly,
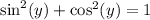
So:
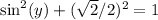
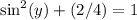
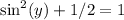
Collect like terms
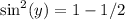
Take LCM
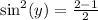
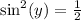
Square roots of both sides
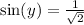
Rationalize
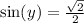
So, we have:
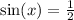
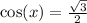
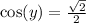
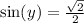
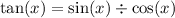
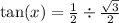
Rewrite as:
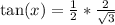
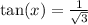
Rationalize
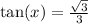
Similarly
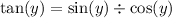
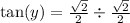
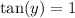
Lastly,
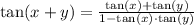
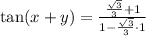
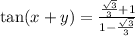
Combine fractions
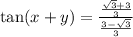
Cancel out 3
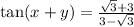
Using a calculator