Question

18

The length of a rectangle is twice as long as the width of the rectangle.
The area of the rectangle is 32 cm.
Draw the rectangle on the centimetre grid.
.
4
54
B2
%

I did it wrong can someone help me

Answer 1

Width = 4 cm

Length = 8 cm

Explanation:

Hi there!

Let
`l` be equal to the length of the rectangle.

Let
`w` be equal to the width of the rectangle.

1) Determine equations to find the length and width

We're given that the length is two times the length of the width:

`l=2w`

We're also given that the area of the rectangle is 32 cm². Recall that the area of a rectangle is
`A=lw`:

`A=lw\\32=lw`

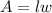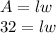
Now, we have our two equations:

`\displaystyle \left \{ {{l=2w} \atop {32=lw}} \right.`

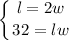
2) Solve for the width using substitution

`\displaystyle \left \{ {{l=2w} \atop {32=lw}} \right.`

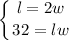
Replace
`l` in the second equation with
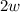`2w` from the first equation:

`32=(2w)w\\32=2w^2`

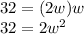
Divide both sides by 2 to isolate w²:

`16=w^2`

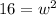
Take the square root of both sides to isolate w:

`\pm4=w`

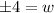
Because width cannot be negative, w=4. Therefore, the width of the rectangle is 4 cm.

3) Solve for the length

`\displaystyle \left \{ {{l=2w} \atop {32=lw}} \right.`

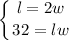
Now, that we have the width (4 cm), we can solve for the length by plugging it back into one of the equations. Either of the equations work, but we can use the first:

`l=2w\\l=2(4)\\l=8`

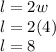
Therefore, the length of the rectangle is 8 cm.

3) Draw the rectangle

We can use what you had before as a foundation. You drew a rectangle with width 4 cm and length 7 cm. To draw the correct rectangle, add another row on top to make it 4 cm by 8 cm.

I hope this helps!