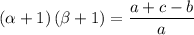Question

The equation a
`x^(2)`+b
`x`+c=0 has roots α, β. Express (α+1)(β+1) in terms of a, b and c.

Answer 1

`\displaystyle \left(\alpha+1\right)\left(\beta + 1\right) = (a+c-b)/(a)\:\: \left(\text{ or } 1+(c-b)/(a)\right)`

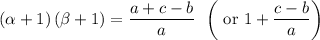
Explanation:

We are given the equation:

`ax^2+bx+c=0`

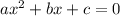
Which has roots α and β.

And we want to express (α + 1)(β + 1) in terms of a, b, and c.

From the quadratic formula, we know that the two solutions to our equation are:

`\displaystyle x_1 = (-b+√(b^2-4ac))/(2a)\text{ and } x_2=(-b-√(b^2-4ac))/(2a)`

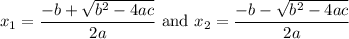
Let x₁ = α and x₂ = β. Substitute:

`\displaystyle \left((-b+√(b^2-4ac))/(2a) + 1\right) \left((-b-√(b^2-4ac))/(2a)+1\right)`

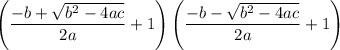
Combine fractions:

`\displaystyle =\left((-b+2a+√(b^2-4ac))/(2a) \right) \left((-b+2a-√(b^2-4ac))/(2a)\right)`

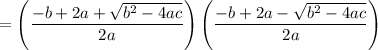
Rewrite:

`\displaystyle = (\left(-b+2a+√(b^2-4ac)\right)\left(-b+2a-√(b^2-4ac)\right))/((2a)(2a))`

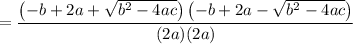
Multiply and group:

`\displaystyle = (((-b+2a)+√(b^2-4ac))((-b+2a)-√(b^2-4ac)))/(4a^2)`

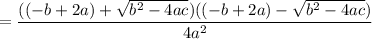
Difference of two squares:

`\displaystyle = \frac{\overbrace{(-b+2a)^2 - (√(b^2-4ac))^2}^((x+y)(x-y)=x^2-y^2)}{4a^2}`

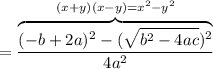
Expand and simplify:

`\displaystyle = ((b^2-4ab+4a^2)-(b^2-4ac))/(4a^2)`

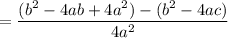
Distribute:

`\displaystyle = ((b^2-4ab+4a^2)+(-b^2+4ac))/(4a^2)`

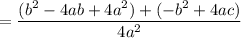
Cancel like terms:

`\displaystyle = (4a^2+4ac-4ab)/(4a^2)`

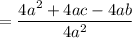
Factor:

`\displaystyle =(4a(a+c-b))/(4a(a))`

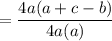
Cancel. Hence:

`\displaystyle = (a+c-b)/(a)\:\: \left(\text{ or } 1+(c-b)/(a)\right)`

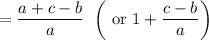
Therefore:

`\displaystyle \left(\alpha+1\right)\left(\beta + 1\right) = (a+c-b)/(a)`