Answer:
d = -1 m
The negative sign indicates that the charge from that force of the space of the two spheres.
Step-by-step explanation:
That is a problem of electric forces, given by Coulomb's law
F =
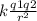
We use that charges of the same sign repel and charges of different signs do not attract, so the net force is
∑ = F₁₃ + F₂₃
F_ {net} =
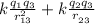
a) the charge is placed at the midpoint between the other two
r₁₃ = r₁₂ = R = ½ m = 0.5m
F_ {net} =
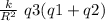
calculate us
F_ {net} = 9 10⁹ / 0.5² 2 10⁻⁶ (50 -25) 10⁻⁶
F_ {net} = 1,800 N
b) where must be placed q3 so that the force is zero
for this case the charge q3 is outside the spheres
∑ F = 0
F₁₁₃ = F₂₃
k q_1 / r_{13}² = k q₂ q₃ / r₂₃²
q₁/ r₁₂² = q₂ / r₂₃²
suppose the distance
r₁₂ = d
the he other sphere is
r₂₃ = d + 1
we substitute
q₃ / d² = q₂ / (d + 1) ²
(d + 1) ² = q₂ / q₃ d²
d² (1 - q₂/ q₃) + 2d + 1 = 0
we solve the equation of a second
d = [-2 +
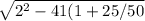 ] / 2
] / 2
d = -2 /2
d = -1 m
The negative sign indicates that the charge from that force of the space of the two spheres.