Question

the tens digit of a two digit number is 5 greater the units digit. If you subtract double the reversed number from it, the result is a fourth of the original number. Find the original number.

Answer 1

Given:

The tens digit of a two digit number is 5 greater the units digit.

If you subtract double the reversed number from it, the result is a fourth of the original number.

To find:

The original number.

Solution:

Let n be the two digit number and x be the unit digit. Then tens digit is (x+5) and the original number is:

`n=(x+5)* 10+x* 1`

`n=10x+50+x`

`n=11x+50`

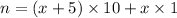
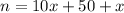
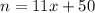
Reversed number is:

`x* 10+(x+5)* 1=10x+x+5`

`x* 10+(x+5)* 1=11x+5`

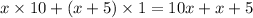
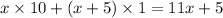
If you subtract double the reversed number from it, the result is a fourth of the original number.

`11x+50-2(11x+5)=(1)/(4)(11x+50)`

`11x+50-22x-10=(1)/(4)(11x+50)`

`40-11x=(1)/(4)(11x+50)`

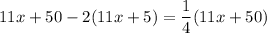
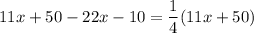
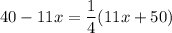
Multiply both sides by 4.

`160-44x=11x+50`

`160-50=11x+44x`

`110=55x`

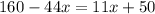
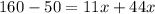
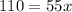
Divide both sides by 55.

`(110)/(55)=x`

`2=x`

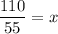
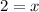
The unit digit is 2. So, the tens digit is
`2+5=7`.

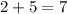Therefore, the original number is 72.