Question

Describe the steps to dividing imaginary numbers and complex numbers with two terms in the denominator?

Answer 1

Let be a rational complex number of the form
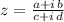`z = (a + i\,b)/(c + i\,d)`, we proceed to show the procedure of resolution by algebraic means:

1)
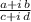`(a + i\,b)/(c + i\,d)` Given.

2)
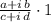`(a + i\,b)/(c + i\,d) \cdot 1` Modulative property.

3)
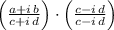`\left((a+i\,b)/(c + i\,d) \right)\cdot \left((c-i\,d)/(c-i\,d) \right)` Existence of additive inverse/Definition of division.

4)
`((a+i\,b)\cdot (c - i\,d))/((c+i\,d)\cdot (c - i\,d))`
`(x)/(y)\cdot (w)/(z) = (x\cdot w)/(y\cdot z)`

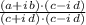
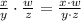
5)
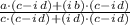`(a\cdot (c-i\,d) + (i\,b)\cdot (c-i\,d))/(c\cdot (c-i\,d)+(i\,d)\cdot (c-i\,d))` Distributive and commutative properties.

6)
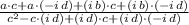`(a\cdot c + a\cdot (-i\,d) + (i\,b)\cdot c +(i\,b) \cdot (-i\,d))/(c^(2)-c\cdot (i\,d)+(i\,d)\cdot c+(i\,d)\cdot (-i\,d))` Distributive property.

7)
`(a\cdot c +i\,(-a\cdot d) + i\,(b\cdot c) +(-i^(2))\cdot (b\cdot d))/(c^(2)+i\,(c\cdot d)+[-i\,(c\cdot d)] +(-i^(2))\cdot d^(2))` Definition of power/Associative and commutative properties/
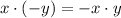`x\cdot (-y) = -x\cdot y`/Definition of subtraction.

8)
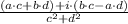`((a\cdot c + b\cdot d) +i\cdot (b\cdot c -a\cdot d))/(c^(2)+d^(2))` Definition of imaginary number/
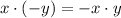`x\cdot (-y) = -x\cdot y`/Definition of subtraction/Distributive, commutative, modulative and associative properties/Existence of additive inverse/Result.

Explanation:

Let be a rational complex number of the form
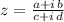`z = (a + i\,b)/(c + i\,d)`, we proceed to show the procedure of resolution by algebraic means:

1)
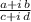`(a + i\,b)/(c + i\,d)` Given.

2)
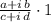`(a + i\,b)/(c + i\,d) \cdot 1` Modulative property.

3)
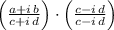`\left((a+i\,b)/(c + i\,d) \right)\cdot \left((c-i\,d)/(c-i\,d) \right)` Existence of additive inverse/Definition of division.

4)
`((a+i\,b)\cdot (c - i\,d))/((c+i\,d)\cdot (c - i\,d))`
`(x)/(y)\cdot (w)/(z) = (x\cdot w)/(y\cdot z)`

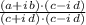
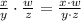
5)
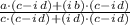`(a\cdot (c-i\,d) + (i\,b)\cdot (c-i\,d))/(c\cdot (c-i\,d)+(i\,d)\cdot (c-i\,d))` Distributive and commutative properties.

6)
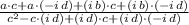`(a\cdot c + a\cdot (-i\,d) + (i\,b)\cdot c +(i\,b) \cdot (-i\,d))/(c^(2)-c\cdot (i\,d)+(i\,d)\cdot c+(i\,d)\cdot (-i\,d))` Distributive property.

7)
`(a\cdot c +i\,(-a\cdot d) + i\,(b\cdot c) +(-i^(2))\cdot (b\cdot d))/(c^(2)+i\,(c\cdot d)+[-i\,(c\cdot d)] +(-i^(2))\cdot d^(2))` Definition of power/Associative and commutative properties/
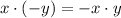`x\cdot (-y) = -x\cdot y`/Definition of subtraction.

8)
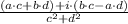`((a\cdot c + b\cdot d) +i\cdot (b\cdot c -a\cdot d))/(c^(2)+d^(2))` Definition of imaginary number/
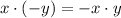`x\cdot (-y) = -x\cdot y`/Definition of subtraction/Distributive, commutative, modulative and associative properties/Existence of additive inverse/Result.