Question

A group of rowdy teenagers near a wind turbine decide to place a pair of

pink shorts on the tip of one blade. They notice that the shorts are at its
maximum height of 16 metres at t = 10 s and its minimum height of 2 metres at
t = 25 s.

a) Determine the equation of the sinusoidal function that describes
the height of the shorts in terms of time.

b) Determine the height of the shorts at exactly t = 10 minutes, to
the nearest tenth of a metre.

Answer 1

a) Hence the equation of the sinusoidal function that describes the height of the shorts in terms of time is
`y = 9 + 7* sin(\pi * t / 15 - \pi / 6)`

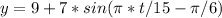
b) Hence the height of the shorts at exactly t = 10 minutes, to

the nearest tenth of a meter is 5.5 meters

Explanation:

a) The wind turbine blade traverses a circular path as it rotates with time (t), whose time variation is given by the following trajectory equation :

`x^2 + (y-yc)^2 = R^2` ,

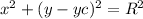where

R = (16 m - 2 m)/2 (since diameter = maximum height - minimum height of the pink short)

= 14 m / 2

= 7 m (radius of the circle)

Also, center of the circle will be at (0, 2 + R) i.e (0,9)

So, is the trajectory path equation to the circle

Let
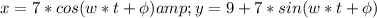`x = 7* cos(w*t + \phi ) & y = 9 + 7* sin(w* t + \phi)` be the parametric form of the above circle equation which represent the position of the pink shorts at the tip of the blade at time t

At t= 10s, y = 16 m so we have,

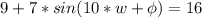`9 + 7 * sin(10* w + \phi) = 16` ---------------(1)

Also, at t= 25s, y =2 m so we have,

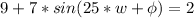`9 + 7* sin(25 * w +\phi) = 2`--------------(2)

Solving we have,
`10* w + \phi = \pi/2 & 25*w + \phi = 3*pi/2`

`15* w = \pi\\\\w = \pi/15 & \phi = \pi/2 - 10*\pi/15 = -\pi / 6`

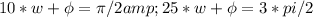
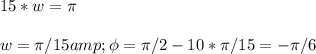
Therefore
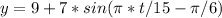`y = 9 + 7* sin(\pi * t / 15 - \pi / 6)` is the instantaneous height of the pink short at time t ( in seconds)

b) At t= 10minutes = 10 * 60 s = 600s, we have,

`y = 9 + 7 * sin(\pi * 600/15 - \pi / 6)\\\\= 9 + 7 * sin(40* \pi - \pi / 6)`

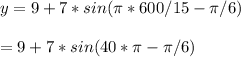
= 5.5 meters (pink short will be at 5.5 meters above ground level at t= 10 minutes)