Question

By method of dimension show that the following equation are homogenous.

i) H=u² sin²Φ/2g
ii)F=Gm1m2/r²​

Answer 1

Proof in explanataion

Step-by-step explanation:

The basic dimensions are as follows:

MASS = M

LENGTH = L

TIME = T

i)

Given equation is:

`H = (u^2Sin^2\phi)/(2g)`

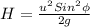
where,

H = height (meters)

u = speed (m/s)

g = acceleration due to gravity (m/s²)

Sin Ф = constant (no unit)

So there dimensions will be:

H = [L]

u = [LT⁻¹]

g = [LT⁻²]

Sin Ф = no dimension

Therefore,

`[L] = ([LT^(-1)]^2)/([LT^(-2)])\\\\\ [L] = [L^((2-1))T^((-2+2))]`

[L] = [L]

Hence, the equation is proven to be homogenous.

ii)

`F = (Gm_1m_2)/(r^2)\\\\`

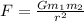
where,

F = Force = Newton = kg.m/s² = [MLT⁻²]

G = Gravitational Constant = N.m²/kg² = (kg.m/s²)m²/kg² = m³/kg.s²

G = [M⁻¹L³T⁻²]

m₁ = m₂ = mass = kg = [M]

r = distance = m = [L]

Therefore,

`[MLT^(-2)] = ([M^(-1)L^(3)T^(-2)][M][M])/([L]^2)\\\\\ [MLT^(-2)] = [M^((-1+1+1))L^((3-2))T^(-2)]\\\\`

[MLT⁻²] = [MLT⁻²]

Hence, the equation is proven to be homogenous.