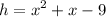Answer:
The expression for the height of the solid is:
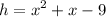
Explanation:
Recall that the volume of a rectangular solid is given by:
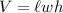
Where l is the length, w is the width, and h is the height.
We know that the volume is given by the polynomial:
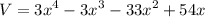
And that the length and width are given by, respectively:
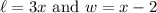
Substitute:
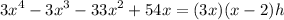
We can solve for h. First, divide both sides by 3x:
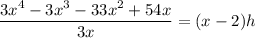
Divide each term:
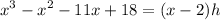
To solve for h, divide both sides by (x - 2):
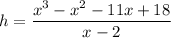
Since this is a polynomial divided by a binomial in the form of (x - a), we can use synthetic division, where a = 2. This is shown below. Therefore, the expression for the height of the solid is: