Question

Mass A, 2.0 kg, is moving with an initial velocity of 15 m/s in the x-direction, and it collides with mass M, 4.0 kg, initially moving at 7.0 m/s in the x-direction. After the collision, the two objects stick together and move as one. What is the change in kinetic energy of the system as a result of the collision, in joules

Answer 1

the change in the kinetic energy of the system is -42.47 J

Step-by-step explanation:

Given;

mass A, Ma = 2 kg

initial velocity of mass A, Ua = 15 m/s

Mass M, Mm = 4 kg

initial velocity of mass M, Um = 7 m/s

Let the common velocity of the two masses after collision = V

Apply the principle of conservation of linear momentum, to determine the final velocity of the two masses;

`M_aU_a + M_mU_m = V(M_a + M_m)\\\\(2* 15 )+ (4* 7) = V(2+4)\\\\58 = 6V\\\\V = (58)/(6) = 9.67 \ m/s`

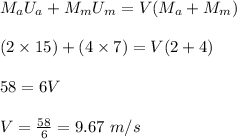
The initial kinetic of the two masses;

`K.E_i = (1)/(2) M_aU_a^2 \ + \ (1)/(2) M_mU_m^2\\\\K.E_i = (0.5 * 2* 15^2) \ + \ (0.5 * 4* 7^2)\\\\K.E_i = 323 \ J`

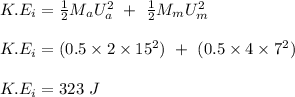
The final kinetic energy of the two masses;

`K.E_f = (1)/(2) M_aV^2 \ + \ (1)/(2) M_mV^2\\\\K.E_f = (1)/(2) V^2(M_a + M_m)\\\\K.E_f = (1)/(2) * 9.67^2(2+ 4)\\\\K.E_f = 280.53 \ J`

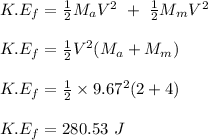
The change in kinetic energy is calculated as;

`\Delta K.E = K.E_f \ - \ K.E_i\\\\\Delta K.E = 280.53 \ J \ - \ 323 \ J\\\\\Delta K.E = -42.47 \ J`

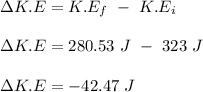
Therefore, the change in the kinetic energy of the system is -42.47 J