Question

B. Projectile on cliff (range)

An object of mass 5 kg is projected at an angle of 25° to the horizontal with a speed of 22 ms-1 from the top of the cliff.
The height of the cliff is 21 m. Take g, the acceleration due to gravity, to be 9.81 ms2
How far horizontally (to 1 decimal place) from the base of the cliff does the object land?

Answer 1

x = 41.28 m

Step-by-step explanation:

This is a projectile launching exercise, let's find the time it takes to get to the base of the cliff.

Let's start by using trigonometry to find the initial velocity

cos 25 = v₀ₓ / v₀

sin 25 = Iv_{oy} / v₀

v₀ₓ = v₀ cos 25

v_{oy} = v₀ sin 25

v₀ₓ = 22 cos 25 = 19.94 m / s

v_{oy} = 22 sin 25 = 0.0192 m / s

let's use movement on the vertical axis

y = y₀ + v_{oy} t - ½ g t²

when reaching the base of the cliff y = 0 and the initial height is y₀ = 21 m

0 = 21 + 0.0192 t - ½ 9.81 t²

4.905 t² - 0.0192 t - 21 = 0

t² - 0.003914 t - 4.2813 =0

we solve the quadratic equation

t =
`( 0.003914\ \pm √(0.003914^2 + 4 \ 4.2813 ) )/(2)`

t =
`(0.003914 \ \pm 4.13828)/(2)`

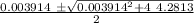
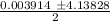
t₁ = 2.07 s

t₂ = -2.067 s

since time must be a positive scalar quantity, the correct result is

t = 2.07 s

now we can look up the distance traveled

x = v₀ₓ t

x = 19.94 2.07

x = 41.28 m