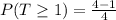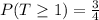Two coins are tossed. Assume that each event is equally likely to occur. a) Use the counting principle to determine the number of sample points in the sample space. b) Construct a tree diagram and list - QAmmunity.org

Two coins are tossed. Assume that each event is equally likely to occur. a) Use the counting principle to determine the number of sample points in the sample space. b) Construct a tree diagram and list

Egor Neliuba asked Nov 6, 2022

480,370 views

1 Answer

Answer:

(a) 4 sample points

(b) See attachment for tree diagram

(c) The probability that no tail is appeared is 1/4

(d) The probability that exactly 1 tail is appeared is 1/2

(e) The probability that 2 tails are appeared is 1/4

(f) The probability that at least 1 tail appeared is 3/4

Explanation:

Given

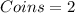
Coins = 2

Solving (a): Counting principle to determine the number of sample points

We have:

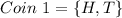
$Coin\ 1 = \{H,T\}$

$Coin\ 2 = \{H,T\}$

To determine the sample space using counting principle, we simply pick one outcome in each coin. So, the sample space (S) is:

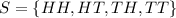
$S = \{HH,HT,TH,TT\}$

The number of sample points is:

n(S) = 4

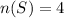
Solving (b): The tree diagram

See attachment for tree diagram

From the tree diagram, the sample space is:

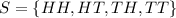
$S = \{HH,HT,TH,TT\}$

Solving (c): Probability that no tail is appeared

This implies that:

P(T = 0)

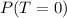
From the sample points, we have:

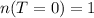n(T = 0) = 1 --- i.e. 1 occurrence where no tail is appeared

So, the probability is:

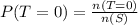
P(T = 0) = (n(T = 0))/(n(S))

This gives:

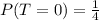
P(T = 0) = (1)/(4)

Solving (d): Probability that exactly 1 tail is appeared

This implies that:

P(T = 1)

From the sample points, we have:

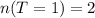n(T = 1) = 2 --- i.e. 2 occurrences where exactly 1 tail appeared

So, the probability is:

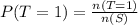
P(T = 1) = (n(T = 1))/(n(S))

This gives:

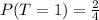
P(T = 1) = (2)/(4)

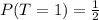
P(T = 1) = (1)/(2)

Solving (e): Probability that 2 tails appeared

This implies that:

P(T = 2)

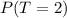
From the sample points, we have:

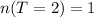n(T = 2) = 1 --- i.e. 1 occurrences where 2 tails appeared

So, the probability is:

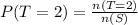
P(T = 2) = (n(T = 2))/(n(S))

This gives:

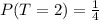
P(T = 2) = (1)/(4)

Solving (f): Probability that at least 1 tail appeared

This implies that:

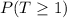
$P(T \ge 1)$

In (c), we have:

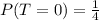
P(T = 0) = (1)/(4)

Using the complement rule, we have:

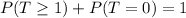
$P(T \ge 1) + P(T = 0) = 1$

Rewrite as:

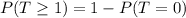
$P(T \ge 1) = 1-P(T = 0)$

Substitute known value

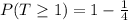
$P(T \ge 1) = 1-(1)/(4)$

Take LCM

$P(T \ge 1) = (4-1)/(4)$

$P(T \ge 1) = (3)/(4)$

Two coins are tossed. Assume that each event is equally likely to occur. a) Use the-example-1

ConnectedSystems answered Nov 13, 2022

by ConnectedSystems

3.1k points

Search QAmmunity.org