Question

System A consists of a mass m attached to a spring with a force constant k; system B has a mass 2m attached to a spring with a force constant k; system C has a mass 3m attached to a spring with a force constant 6k; and system D has a mass m attached to a spring with a force constant 4k. Rank these systems in order of decreasing period of oscillation.

Answer 1

T₂ > T₁ > T₃ >T₄

Step-by-step explanation:

In a simple harmonic motion the angular velocity is

w =
`\sqrt{(k)/(m) }`

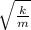
angular velocity and period are related

w = 2π / T

we substitute

T =
`2 \pi \ \sqrt{(m)/(k) }`

let's find the period for each case

a) mass m

spring constant k

T₁ = 2π
`\sqrt{(m)/(k) }`

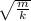
b) mass 2m

spring constant k

T₂ = 2π
`\sqrt{(2m)/(k) }`

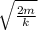
T₂ = T₁ √2

T₂ = T₁ 1.41

c) masses 3m

spring constant 6k

T₃ = 2π
`\sqrt{(3m)/(6k) }`

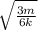
T₃ = 2π
`\sqrt{(m)/(k) } \ √(0.5)`

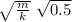
T₃ = T₁ 0.707

d) mass m

spring constant 4k

T₄ = 2π
`\sqrt{ (m)/(4k) }`

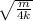
T₄ = 2π
`\sqrt{(m)/(k) } \ √(0.25)`

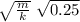
T₄ = T₁ 0.5

now let's order the periods in decreasing order

T₂ > T₁ > T₃ >T₄