Given:
The given expression is:
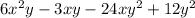
To find:
Part A: The expression by factoring out the greatest common factor.
Part B: Factor the entire expression completely.
Solution:
Part A:
We have,
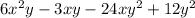
Taking out the highest common factor 3y, we get
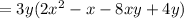
Therefore, the required expression is
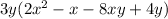 .
.
Part B:
From part A, we have,
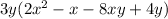
By grouping method, we get
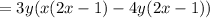

Therefore, the required factored form of the given expression is
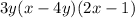 .
.