Question

How many 10-letter words real or imaginary can. Be formed from the following letters R,S,P,Q,H,J,S,M,B,A

Answer 1

Answer: 3628800

Step-by-step explanation: there are 10 letters so we multiply each with the other 1x2x3x4x5x6x7x8x9x10 or 10! to know all possible combinations so the answer will be 3628800.

Hope it helped!

Answer 2

`1,814,400`

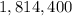
Explanation:

The number of ways to arrange a word with
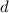`d` distinct digits is each to
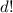`d!`. Since there are 10 letters, there are
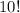`10!` permutations initially formed.

However, there is one letter that is repeated, S. We need to account for that fact that switching the placement of the S's does not change the word, as they still appear the same. Therefore, divide
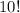`10!` by the number of ways you can arrange the 2 S's, which is simply
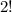`2!`. Therefore, our answer is:

`(10!)/(2!)=10 \cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3=\boxed{1,814,000}`