Answer:
Step-by-step explanation:
Because vectors have direction and x and y components you can't just add them and say that their length is 16 because A is 8 units and so is B. What you're actually finding is the magnitude and direction of the vector that results from this addition. The magnitude is the length of the resultant vector, which comes from the x and y components of A and B, and the direction is the angle between the resultant vector and the positive x axis. To add the vectors, then, we need to find the x and y components of each. We'll do the x components of A and B first so we can add them to get the x component of C. Since x values are directly related to cos, the formula to find the x components of vectors is
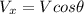 which is the magnitude of the vector (its length) and the angle. Finding the x components of A:
which is the magnitude of the vector (its length) and the angle. Finding the x components of A:
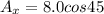 so
so
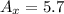 and for B:
and for B:
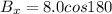 since the negative x axis is the 180 degree axis and
since the negative x axis is the 180 degree axis and
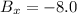 If we add them, we get
If we add them, we get
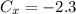
Now onto the y components. The formula for that is almost the same as the x components except use sin instead of cos:
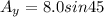 so
so
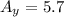 and
and
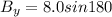 so
so
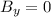 If we add them, we get
If we add them, we get
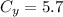
Now for the final magnitude:
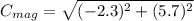 and
and
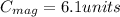 and now onto the direction.
and now onto the direction.
The x component of C is positive and the y component is negative, which means that the direction has us at an angle is quadrant 2; we add 180 to whatever the angle is. Finding the angle:
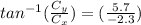 = -68 + 180 = 112 degrees
= -68 + 180 = 112 degrees
The resultant vector of A + B has a magnitude of 6.1 and a direction of 112°
Do the same thing for subtraction, except if you're subtracting B from A, the direction that B is pointing has to go the opposite way. That means that A doesn't change anything at all, but B is now pointing towards 0.
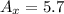 (doesn't change from above)
(doesn't change from above)
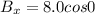 and
and
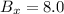 so
so
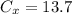 and
and
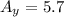 (also doesn't change from above)
(also doesn't change from above)
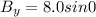 so
so
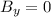 and
and
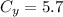 and for the magnitude:
and for the magnitude:
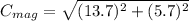 so
so
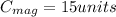 and for the direction:
and for the direction:
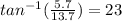 and since both x and y components of C are in Q1, we add nothing.
and since both x and y components of C are in Q1, we add nothing.
And you're done!!!