Question

Please help me i will give 20 points for this question ​

Answer 1

1. a. 2

b. -½

c. y - 3 = -½(x - 8) => point-slope form

y = -½x + 7 => slope-intercept form

2. a. -1

b. 1

c. y - 5 = 1(x - 3) => point-slope form

y = x + 2 => slope-intercept form

Explanation:

1. (8, 3) and (10, 7):

a. The gradient for the line joining the points:

Gradient =
`(y_2 - y_1)/(x_2 - x_1)`

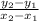
Let,

`(8, 3) = (x_1, y_1)`

`(10, 7) = (x_2, y_2)`

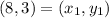
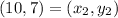
Plug in the values

Gradient =
`(7 - 3)/(10 - 8)`

Gradient =
`(4)/(2)`

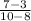
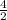
Gradient = 2

b. The gradient of the line perpendicular to this line = the negative reciprocal of 2

Negative reciprocal of 2 = -½

c. The equation of perpendicular line if it passes through the first point, (8, 3):

Equation of the perpendicular line in point-slope form can be expressed as y - b = m(x - a).

Where,

(a, b) = (8, 3)

Slope (m) = -½

Substitute (a, b) = (8, 3), and m = -½ into the point-slope equation, y - b = m(x - a).

Thus:

y - 3 = -½(x - 8) => point-slope form

We cam also express the equation of the perpendicular line in slope-intercept form by rewriting y - 3 = -½(x - 8) in the form of y = mx + b:

Thus:

y - 3 = -½(x - 8)

y - 3 = -½x + 4

y - 3 + 3 = -½x + 4 + 3

y = -½x + 7

2. (3, 5) and (4, 4):

a. The gradient for the line joining the points:

Gradient =
`(y_2 - y_1)/(x_2 - x_1)`

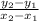
Let,

`(3, 5) = (x_1, y_1)`

`(4, 4) = (x_2, y_2)`

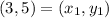
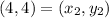
Plug in the values

Gradient =
`(4 - 5)/(4 - 3)`

Gradient =
`(-1)/(1)`

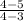
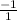
Gradient = -1

b. The gradient of the line perpendicular to this line = the negative reciprocal of -1

Negative reciprocal of -1 = 1

c. The equation of perpendicular line if it passes through the first point, (3, 5):

Equation of the perpendicular line in point-slope form can be expressed as y - b = m(x - a).

Where,

(a, b) = (3, 5)

Slope (m) = 1

Substitute (a, b) = (3, 5), and m = 1 into the point-slope equation, y - b = m(x - a).

Thus:

y - 5 = 1(x - 3) => point-slope form

We can also express the equation of the perpendicular line in slope-intercept form by rewriting y - 5 = 1(x - 3) in the form of y = mx + b:

Thus:

y - 5 = 1(x - 3)

y - 5 = x - 3

y - 5 + 5 = x - 3 + 5

y = x + 2