Answer:
See explanation.
General Formulas and Concepts:
Algebra I
- Terms/Coefficients
- Factoring
Algebra II
Pre-Calculus
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Property [Multiplied Constant]:
![\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/sajvvpx1sytxjokl40ke2f.png)
Derivative Property [Addition/Subtraction]:
![\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/iqt7axoe8j2sh12ig7n0ah.png)
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Quotient Rule]:
![\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/u1jpwlo9x561ji74gvehcp.png)
Parametric Differentiation:
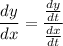
Explanation:
Step 1: Define
Identify
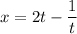
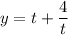
Step 2: Find Derivative
- [x] Differentiate [Basic Power Rule and Quotient Rule]:
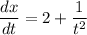
- [y] Differentiate [Basic Power Rule and Quotient Rule]:
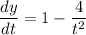
- Substitute in variables [Parametric Derivative]:
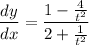
- [Parametric Derivative] Simplify:
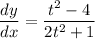
- [Parametric Derivative] Polynomial Long Division:
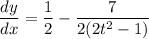
- [Parametric Derivative] Factor:
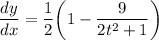
Here we see that if we increase our values for t, our derivative would get closer and closer to 0.5 but never actually reaching it. Another way to approach it is to take the limit of the derivative as t approaches to infinity. Hence
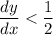 .
.
Topic: AP Calculus BC (Calculus I + II)
Unit: Parametrics
Book: College Calculus 10e