Answer:
The car skids in a distance of 61.275 meters.
Step-by-step explanation:
Since the only force exerted on the car is the kinetic friction between the car and the horizontal road, deceleration of the vehicle (
 ), measured in meters per square second, is determined by the following expression:
), measured in meters per square second, is determined by the following expression:
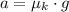 (1)
(1)
Where:
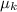 - Coefficient of kinetic friction, no unit.
- Coefficient of kinetic friction, no unit.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
If we know that
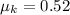 and
and
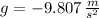 , then the net deceleration of the vehicle is:
, then the net deceleration of the vehicle is:
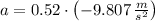
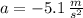
The distance covered by the car is finally calculated by this kinematic expression:
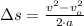 (2)
(2)
Where:
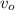 ,
,
 - Initial and final speed, measured in meters per second.
- Initial and final speed, measured in meters per second.
 - Net deceleration, measured in meters per square second.
- Net deceleration, measured in meters per square second.
If we know that
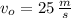 ,
,
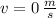 and
and
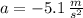 , then the distance covered by the car is:
, then the distance covered by the car is:
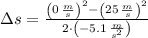
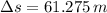
The car skids in a distance of 61.275 meters.