Question

(4 pts) If a rock is thrown vertically upward from the surface of Mars with an initial velocity of 15m/sec

then the height of the rock after t seconds is h=15t-1.86t^2 (h in meters and t in seconds). The
rock will reach its maximum height when the velocity=0 m/sec. How long does it take for the rock to
reach its maximum height, and what is the maximum height?

Answer 1

Explanation:

I see you're in college math, so we'll solve this with calculus, since it's the easiest way anyway.

The position equation is

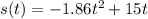`s(t)=-1.86t^2+15t` That equation will give us the height of the rock at ANY TIME during its travels. I could find the height at 2 seconds by plugging in a 2 for t; I could find the height at 12 seconds by plugging in a 12 for t, etc.

The first derivative of position is velocity:

v(t) = -3.72t + 15 and you stated that the rock will be at its max height when the velocity is 0, so we plug in a 0 for v(t):

0 = -3.72t + 15 and solve for t:\

-15 = -3.72t so

t = 4.03 seconds. This is how long it takes to get to its max height. Knowing that, we can plug 4.03 seconds into the position equation to find the height at 4.03 seconds:

s(4.03) = -1.86(4.03)² + 15(4.03) so

s(4.03) = 30.2 meters.

Calculus is amazing. Much easier than most methods to solve problems like this.