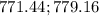Answer:
The correct answer is "771.44; 779.16".
Explanation:
Given:
Number of samples,
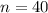
Mean,
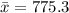
Standard deviation,
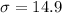
At 90% confidence interval,

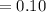
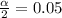
From normal distribution at 90% confidence level,
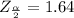
Now,
Margin of error will be:
⇒
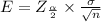
By substituting the values, we get
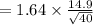
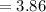
hence,
The mean at 90% CI will be:
=
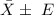
=
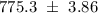
=