Question

.. A cistern has two pipes. The first and second pipes can fill the empty cistern in 12 hours and 18 hours respectively. If both pipes are opened together, how much time will the empty cistern need in order to be filled?​

Answer 1

`7.2\; \text{hours}`.

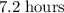Explanation:

Let the volume of this cistern be
`1`.

The first pipe fills the cistern at a rate of
`\displaystyle \frac{1}{12\; \text{hour}}`.

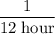In other words, each hour, the first pipe would fill
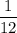`\displaystyle (1)/(12)` of the cistern every hour.

On the other hand, the second pipe fills the cistern at a rate of
`\displaystyle \frac{1}{18\; \text{hour}}`.

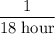This pipe would fill
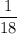`\displaystyle (1)/(18)` of the cistern every hour.

Hence, when opened together, the two pipes would fill
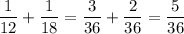`\displaystyle (1)/(12) + (1)/(18) = (3)/(36) + (2)/(36) = (5)/(36)` of this cistern every hour.

At this rate, it would take
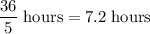`\displaystyle (36)/(5)\; \text{hours} = 7.2\; \text{hours}` for the two pipes to fill the entire cistern.