Answer:
(a) There are outliers
(b)
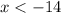 and
and

Explanation:
Given
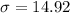
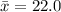
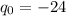
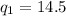
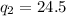
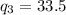
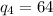
Solving (a): Check for outliers
This is calculated using:
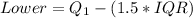 --- lower bound of outlier
--- lower bound of outlier
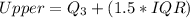 --- upper bound of outlier
--- upper bound of outlier
Where

So, we have:
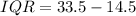

The lower bound of outlier becomes
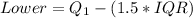
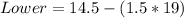
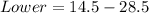

The upper bound of outlier becomes
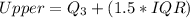
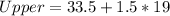

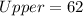
So, we have:
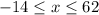 --- the range without outlier
--- the range without outlier
Given that:
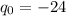 --- This represents the lowest data
--- This represents the lowest data
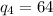 --- This represents the highest data
--- This represents the highest data
-24 and 64 are out of range of
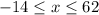 .
.
Hence, there are outliers
Solving (b): The outliers
The outliers are data less than the lower bound (i.e. less than -14) or greater than the upper bound (i.e. 62)
So, the outliers are:
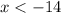 and
and
