Question

△ABCis reflected to form​​ ​△A′B′C′​. The vertices of △ABC are A(3, 1), B(1, 5), and C(6, 9). The vertices of △A′B′C′ are A′(−1, −3), B′(−5, −1), and C′(−9, −6). Which reflection results in the transformation of ​△ABC​​ to ​△A′B′C′​​? Reflection across the x-axis reflection across the y-axis reflection across y = x reflection across y=−x I NEED HELP PLS The answer choies are: A. Reflection across the x-axis B. Reflection across the y-axis C. Reflection across y = x D. Reflection across y=−x

Answer 1

Answer: D) reflection across y = -x

Step-by-step explanation:

When we reflect over y = x, we basically swap x and y. So for instance, the point (3,1) becomes (1,3).

When reflecting over y = -x, we will do the same thing but we'll make each coordinate swap in sign from positive to negative (or vice versa). The rule for reflecting over y = -x is
`(x,y) \to (-y,-x)`

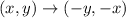
So if we apply that rule to point A(3,1) then it becomes A ' (-1, -3).

Similarly, B(1,5) moves to B ' (-5, -1)

Finally, C(6,9) becomes C ' (-9, -6)