Question

Jane begins filling a large jug with water, using a faucet that dispenses 3.5 liters of water per minuteAfter 1 minute, Ariel begins filling her jug of the same size, using a faucet that dispenses. 4 liters of water per minute.How many minutes will it take for the water in Ariel's tub to reach the level of Jane's and how much water will each hold at the time?

Answer 1

It takes 8 minutes for each of them to have 28 liters

=======================================================

Step-by-step explanation:

• x = time that has elapsed (in minutes) since Jane started filling her jug
• y = amount of water in the jug (in liters)

x and y are nonnegative real numbers.

The equation for Jane is y = 3.5x since her faucet has a rate of 3.5 liters per min.

For example, if x = 2 minutes go by, then y = 3.5*x = 3.5*2 = 7 liters are filled up.

-----------------------

We're told that after 1 minute Jane has started, Ariel has started to fill her jug. This must mean Ariel's time value is x-1. Whatever Jane's time value is, subtract off 1. This is because Jane has the 1 minute head start.

The equation for Ariel is y = 4(x-1) since her faucet has a rate of 4 liters per min.

----------------------

The system of equations to solve is

`\begin{cases}y = 3.5x\\y = 4(x-1)\end{cases}`

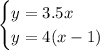
Let's apply substitution to solve for x.

y = 3.5x

4(x-1) = 3.5x

4x-4 = 3.5x

4x-3.5x = 4

0.5x = 4

x = 4/0.5

x = 8

At the 8 minute mark (ie 8 minutes after Jane starts), is when the two jugs will have the same amount of water.

• Jane: y = 3.5x = 3.5*8 = 28
• Ariel: y = 4(x-1) = 4(8-1) = 4(7) = 28

Both of them have 28 liters each.