Question

If four items are chosen at random without replacement from seven items, in how many ways can the four items be arranged, treating each arrangement as a different event (i.e., if order is important)?

Answer 1

840 ways.

Explanation:

The order is important, which means that the permutations formula is used to solve this question.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

In this question:

4 items from a set of 7, so:

`P_((7,4)) = (7!)/((7-4)!) = 7*6*5*4 = 840`

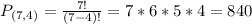
840 ways.