Question

A tractor of mass 2000kg Pulls a trailer of mass 1500kg. The total frictional force is 3000N and the acceleration of the tractor is 3ms^-2. Calculate;

(a) the force exerted on the tractor by the tow-bar when the acceleration is 3ms^-2
(b) the force exerted when the tractor and trailer are moving at a constant speed of 4m/s

Answer 1

a) T = -22796.5 N, b) F = 3000 N

Step-by-step explanation:

a) For this part we use Newton's second law

Let's set a reference frame with the x-axis in the direction of motion and the y-axis in the vertical direction.

We make a free-body diagram for each body,

the tractor has the bar force (T) and the push force (F) and the friction force (fr₁)

Y axis

N₁ -W₁ = 0

N₁ = M₁ g

X axis

F - T - fr₁ = M₁ a

the Trailer has the bar force (T) and the friction force (fr₂)

Y axis

N₂ - W₂ = 0

N₂ = m₂ g

X axis

T - fr₂ = m₂ a

let's write the system of equations

F - T - fr₁ = M₁ a (1)

T - fr₂ = m₂ a

we solve

F - (fr₁ + fr₂) = (M₁ + m₂) a

indicate that the total friction forces are fr = 3000N

fr = fr₁ + fr₂

F =
`((M_1+m_2) a)/(fr)`

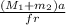
let's calculate

F =
`((2000+1500) \ 3)/(3000)`

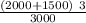
F = 3.5 N

The friction force is

fr = μ N

the norm of the system is N = N₁ + N₂

μ =
`(fr)/(N_1 + N_2)`

μ =
`(3000)/(2000+1500)`

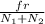
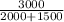
μ = 0.858

with this value we can find the friction force 1 and substitute in equation 1

F - T - μ N₁ = M₁ a

T = F - M₁ (a + μ g)

T = 3.5 - 2000 (3 + 0.858 9.8)

T = -22796.5 N

b) when the system moves with constant velocity the acceleration is zero

F - T - fr₁ = 0

T - fr₂ = 0

we solve

F + (fr₁ + fr₂) = 0

F = fr₁ + fr₂

F = 3000 N