Question

A 59.0 kg bungee jumper jumps off a bridge and undergoes simple harmonic motion. If the period of oscillation is 0.250 mins, what is the spring constant (in N/m) of the bungee cord, assuming it has negligible mass compared to that of the jumper

Answer 1

The spring constant of the bungee cord is approximately 2982 N/m

Step-by-step explanation:

The spring constant (k) of a bungee cord can be calculated using the formula:

k = (4 π^2 * m) / T^2

Where m is the mass of the bungee jumper and T is the period of oscillation.

Substituting the given values, we have:

k = (4 * 3.14^2 * 59.0 kg) / (0.250 mins)^2

Simplifying the expression, we find that the spring constant of the bungee cord is approximately 2982 N/m.

Answer 2

The spring constant of the spring is 10.3 N/m.

Step-by-step explanation:

Given that,

Mass of a bungee jumper, m = 59 kg

The period of oscillation, T = 0.25 min = 15 sec

We need to find the spring constant of the bungee cord. We know that the period of oscillation is given by :

`T=2\pi\sqrt{(m)/(k)}`

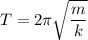
Where

k is the spring constant

`T^2=4\pi^2* (m)/(k)\\\\k=4\pi^2* (m)/(T^2)\\\\k=4\pi^2* (59)/((15)^2)\\\\k=10.3\ N/m`

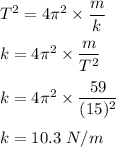
So, the spring constant of the spring is 10.3 N/m.